Ellipse de polarisation
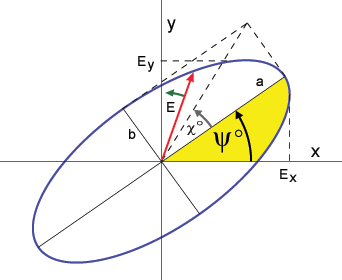
On peut considérer que le champ électrique d'une onde plane est la somme vectorielle de deux composantes orthogonales, habituellement les composantes horizontale et verticale. Ces deux composantes sont caractérisées par leur amplitude et leur différence de phase. Si nous observons l'onde dans la direction de sa propagation, la pointe du vecteur du champ électrique d'une onde complètement polarisée trace une courbe régulière dont la forme la plus générale est l'ellipse. (Cf. figure 1 2).
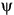 et son ellipticité,
et son ellipticité, 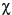 , lesquels sont des fonctions du demi-grand axe, a, et du demi-grand axe, b.
, lesquels sont des fonctions du demi-grand axe, a, et du demi-grand axe, b.L'ellipse possède un demi-grand axe, a, et un demi-petit axe, b. L'angle du demi-grand axe, mesuré dans le sens antihoraire à partir de la moitié positive de l'axe horizontal, est l'orientation, 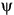 , de l'onde électromagnétique. Sa valeur se situe entre 0° et 180°. L'aplatissement de l'ellipse est décrite par un paramètre nommé ellipticité ou excentricité, défini par
, de l'onde électromagnétique. Sa valeur se situe entre 0° et 180°. L'aplatissement de l'ellipse est décrite par un paramètre nommé ellipticité ou excentricité, défini par 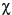 = arctan(b/a). Sa valeur se situe entre -45° et +45°.
= arctan(b/a). Sa valeur se situe entre -45° et +45°.
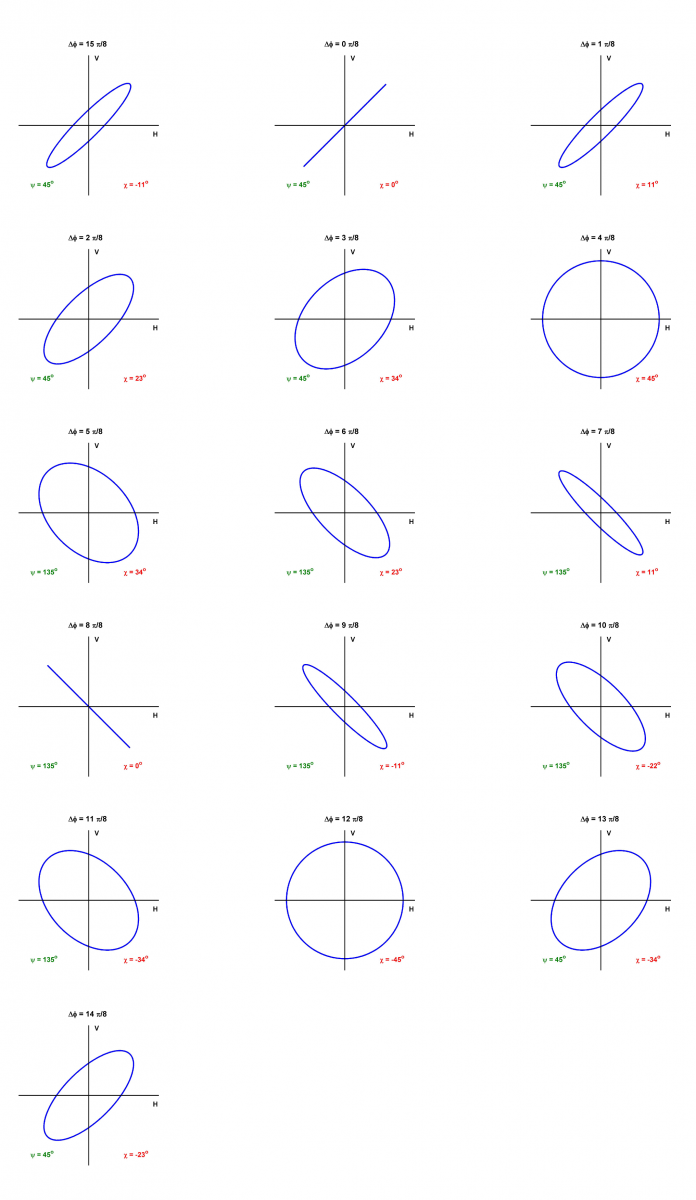
La forme de l'ellipse est régie par l'amplitude et la phase relative des composantes horizontale et verticale du vecteur du champ électrique. La figure 1 3 montre l'effet de la différence de phase entre les composantes pour des amplitudes égales. Lorsque les composantes sont en phase, la polarisation est linéaire (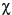 = 0) et l'orientation est de 45°. Si on augmente la différence de phase à
= 0) et l'orientation est de 45°. Si on augmente la différence de phase à 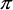 /2 radian, l'orientation demeure à 45°, mais l'ellipticité atteint 45°, l'onde est alors polarisée circulairement. On peut voir cette évolution, par saut de
/2 radian, l'orientation demeure à 45°, mais l'ellipticité atteint 45°, l'onde est alors polarisée circulairement. On peut voir cette évolution, par saut de 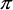 /8 radian, sur la première rangée de la figure 1 3 et la première image de la deuxième rangée.
/8 radian, sur la première rangée de la figure 1 3 et la première image de la deuxième rangée.
Alors que l'on accroît la différence de phase de p/2 à 3p/2 radians, l'orientation passe à 135° et l'ellipticité de +45° à 0° pour atteindre -45°. Cette séquence est visible dans les deuxième et troisième rangées de la figure et la première image de la quatrième. Dans la quatrième rangée, la différence de phase passe de 3p/2 à 15p/8, l'orientation retourne à + 45° et l'ellipticité revient à 0°.
Alors que l'on accroît la différence de phase de 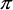 /2 à 3
/2 à 3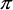 /2 radians, l'orientation passe à 135°, et l'ellipticité de 45° à 0° pour atteindre -45°. Cette séquence est visible dans les deuxième et troisième rangées de la figure et la première image de la quatrième. Dans la quatrième rangée, la différence de phase passe de 3
/2 radians, l'orientation passe à 135°, et l'ellipticité de 45° à 0° pour atteindre -45°. Cette séquence est visible dans les deuxième et troisième rangées de la figure et la première image de la quatrième. Dans la quatrième rangée, la différence de phase passe de 3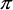 /2 to 15
/2 to 15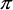 /8, l'orientation retourne à +45°, et l'ellipticité revient à 0°.
/8, l'orientation retourne à +45°, et l'ellipticité revient à 0°.
 /8 radians par sauts de
/8 radians par sauts de  /8
/8Image agrandie
On peut voir à la figure 1-3 que le cercle et le segment de droite sont les cas limites de l'ellipse. Si l'angle de phase entre les composantes horizontale et verticale est 0° ou  radians, l'ellipse devient une ligne droite. Dans ce cas, l'ellipticité est zéro et la polarisation est linéaire.
radians, l'ellipse devient une ligne droite. Dans ce cas, l'ellipticité est zéro et la polarisation est linéaire.
 Le saviez-vous?
Le saviez-vous?On peut produire une onde totalement polarisée à partir d'un mélange d'ondes sinusoïdales de plusieurs fréquences. Cependant, on suppose généralement dans les systèmes de radar à synthèse d'ouverture qu'il n'y a qu'une seule fréquence, en d'autres termes, que l'onde est monochromatique. Cette hypothèse est valide, puisque ces systèmes ont une largeur de bande très étroite (relativement à leur fréquence) et que l'on peut approximer que l'onde transmise est parfaitement sinusoïdale.
Dans la figure 1-3, les amplitudes des composantes horizontale et verticale sont égales. En cas d'inégalité, l'orientation, 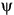 y, peut prendre une valeur entre 0 et 180°. Si l'ellipticité est zéro et l'orientation égale à 0° ou 180°, la polarisation linéaire est horizontale (la composante verticale est nulle). En contrepartie, si
y, peut prendre une valeur entre 0 et 180°. Si l'ellipticité est zéro et l'orientation égale à 0° ou 180°, la polarisation linéaire est horizontale (la composante verticale est nulle). En contrepartie, si 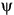 = 90°, l'onde est polarisée linéairement dans l'axe vertical (sa composante horizontale est nulle). On utilise habituellement ces deux polarisations linéaires.
= 90°, l'onde est polarisée linéairement dans l'axe vertical (sa composante horizontale est nulle). On utilise habituellement ces deux polarisations linéaires.
Si l'angle de phase entre les composantes horizontale et verticale est égal à 90°, alors que les composantes horizontale et verticale sont égales, l'ellipse devient un cercle. Dans ce cas, l'ellipticité égale 45° et l'orientation ne peut être définie. Une ellipticité, 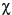 = - 45°, correspond à une polarisation circulaire droite (appelée parfois polarisation dextrogyre). Le vecteur du champ électrique d'une onde polarisée circulairement à gauche, si elle est observée le long de sa propagation, tourne dans le sens antihoraire. (On parle parfois de polarisation lévogyre ou, très rarement, sénestrogyre).
= - 45°, correspond à une polarisation circulaire droite (appelée parfois polarisation dextrogyre). Le vecteur du champ électrique d'une onde polarisée circulairement à gauche, si elle est observée le long de sa propagation, tourne dans le sens antihoraire. (On parle parfois de polarisation lévogyre ou, très rarement, sénestrogyre).
Les figures suivantes montrent les polarisations linéaire, elliptique et circulaire, la rotation du vecteur du champ électrique est aussi illustrée.
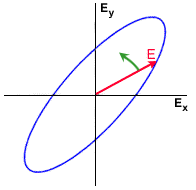
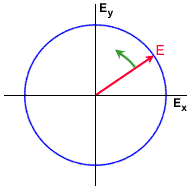
Question éclair

Question: Pourquoi les composantes horizontale et verticale suffisent-elles à décrire la polarisation d'une onde électromagnétique?
Question éclair - réponse

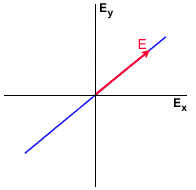
Réponse : La polarisation d'une onde électromagnétique plane est décrite par le lieu tracé par la pointe de son vecteur électrique dans le plan perpendiculaire à sa propagation. Or, dans un plan, deux axes orthogonaux seulement sont nécessaires pour décrire la position d'un vecteur. Les composantes horizontale et verticale Ex et Ey (ou Eh et Ev) sont les plus commodes.
Détails de la page
- Date de modification :