ARCHIVÉE - Analyse des données sur l'énergie
Information archivée dans le Web
Information identified as archived on the Web is for reference, research or recordkeeping purposes. It has not been altered or updated after the date of archiving. Web pages that are archived on the Web are not subject to the Government of Canada Web Standards. As per the Communications Policy of the Government of Canada, you can request alternate formats. Please "contact us" to request a format other than those available.
Aperçu
La présente section, qui porte sur l'analyse des données sur l'énergie, constitue un élément clé de ce guide. L'analyse efficace des données est essentielle mais souvent, on ne lui accorde pas l'importance qui lui revient. En fait, une analyse médiocre peut gravement nuire au bon fonctionnement d'un SIGE et produire des messages pouvant induire en erreur.
Les données sur l'énergie ne se limitent pas à celles sur la consommation; elles comprennent également d'importants facteurs qui influencent celle-ci. La fréquence de saisie des données doit être plus grande que la fréquence des variations étudiées.
L'analyse des données a pour objet de mieux comprendre la consommation et le coût de l'énergie, de calculer les niveaux de rendement et d'établir les objectifs et la consommation modèle. Un éventail de techniques sont disponibles, allant des plus simples aux plus complexes. Ces techniques devraient être choisies en fonction des problèmes à résoudre (au lieu de choisir d'abord une technique d'analyse, puis de trouver une situation qui y correspond).
Le diagramme de la figure 19 résume tous les sujets abordés dans la présente section.
Figure 19. Schéma des éléments d'une analyse des données sur l'énergie
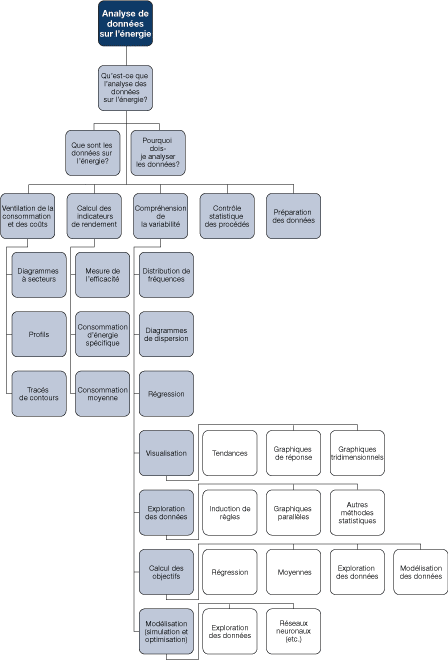
[version textuelle - Figure 19]
8.1 Qu'entend-on par données sur l'énergie?
Les données sur l'énergie comprennent :
- les mesures directes de la consommation de services d'utilité publique (électricité, gaz, vapeur, etc.);
- les mesures directement associées à la consommation d'énergie, par exemple, le taux de chauffage, le taux de refroidissement ou le débit d'air comprimé;
- les facteurs déterminants de la consommation mesurés ou les variables enregistrées pouvant avoir une incidence sur la consommation.
Les mesures directes et indirectes de la consommation d'énergie sont indispensables. Il faudrait calculer séparément la consommation de chaque secteur important du procédé. Un secteur est désigné comme suit :
- un secteur où la consommation d'énergie est principalement déterminée par les actions ayant lieu au sein du secteur, du procédé ou de l'usine;
- un secteur dont la consommation des divers types d'énergie est très élevée;
- un secteur où le rendement est variable ou risque de ne pas être optimal;
- un secteur administré par une personne ou un groupe auquel on peut attribuer la responsabilité du rendement.
Le tableau 5 fournit des exemples de secteurs dont la consommation d'énergie doit être mesurée.
| Tableau 5. Exemples de secteurs dont les services doivent être mesurés |
| Secteur |
|
|
|
| Centrales de cogénération – taux de chauffage |
|
|
|
|
Il est essentiel d'avoir en main des données sur les facteurs déterminants. Sans ces données, l'analyse énergétique se limite à la mesure de la consommation et des coûts, et à la comparaison des valeurs courantes avec les valeurs historiques. Les économies réalisables s'en verraient très réduites. L'utilisation de données sur les facteurs déterminants permet :
- de comprendre les causes d'une consommation variable;
- d'établir des objectifs auxquels on peut comparer les rendements actuels;
- de modéliser la consommation d'énergie.
| Tableau 6. Exemples de facteurs déterminants |
| Perturbations externes |
|
|
|
| Facteurs contrôlables |
|
|
|
|
8.2 Objectifs de l'analyse des données sur l'énergie
Voici les objectifs d'une analyse des données sur l'énergie :
- ventiler la consommation et les coûts d'énergie;
- calculer les niveaux de rendement;
- comprendre pourquoi la consommation d'énergie et le rendement varient;
- calculer, pour la consommation et l'efficacité, des valeurs cibles qui permettront de repérer un rendement insuffisant et d'assurer un suivi;
- modéliser la demande d'énergie.
Les techniques d'analyse des données vont des plus simples aux plus complexes. Celles à choisir dépendent de la taille et de la complexité des opérations, du financement et des outils logiciels disponibles, des compétences et des intérêts du personnel, ainsi que du temps disponible.
8.3 Ventilation de la consommation et des coûts d'énergie
Il y a plusieurs avantages à diviser la consommation totale d'énergie (et les coûts correspondants) d'une installation par sous-secteur :
- répartition des coûts par service;
- mise en relief des secteurs clés;
- incitation à la discussion et à l'émergence de nouvelles idées.
Figure 20. Ventilation de la consommation d'énergie

[version textuelle - Figure 20]
Dans les exemples de la figure 20, on tient compte de l'ensemble des services publics (électricité, gaz, mazout, vapeur, etc.) en fonction des coûts qui leur sont associés.
Des diagrammes basés sur la consommation d'énergie (en MJ, kWh, etc.) ou sur les émissions en équivalent CO2 peuvent aussi être utiles. Ils peuvent éclairer les lecteurs sur la consommation d'énergie selon les divers services publics et les coûts correspondants. Tous ces diagrammes sont essentiels à la gestion de l'énergie. Ils reposent en général sur des données couvrant une période d'un an.
La figure 21 illustre la répartition des services, c'est-à-dire la consommation des divers types d'énergie, et la répartition des coûts correspondante (diagramme de droite). On peut voir que le coût de l'électricité est relativement élevé et que ce coût a des répercussions sur les priorités en matière d'efficacité énergétique.
Figure 21. Répartition des services selon la consommation et les coûts énergétiques
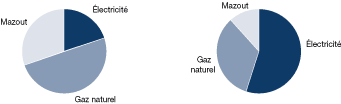
[version textuelle - Figure 21]
Ce type de diagramme peut facilement être produit à l'aide d'un chiffrier courant ou d'un autre logiciel semblable et être publié, par exemple, comme partie intégrante d'une section sur l'énergie de l'intranet de l'entreprise.
Dans certains cas, il peut être utile de ventiler la consommation d'énergie par tranches de temps. Par exemple, il peut être fort utile de déterminer la consommation moyenne pendant les périodes d'arrêt de production (p. ex., nuit, vacances), afin de repérer les opérations dont le contrôle est insuffisant (p. ex., isolation inadéquate de l'air comprimé).
Figure 22. Ventilation mensuelle de la consommation d'électricité illustrant les périodes diurnes et nocturnes
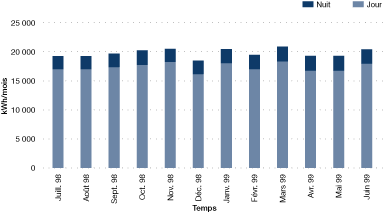
[version textuelle - Figure 22]
La détermination des périodes de pointe permet également d'obtenir des renseignements utiles. Il y aurait lieu, dans la mesure du possible, d'étudier le profil de la demande.
Figure 23a. Profil typique de la demande aux 30 minutes (graphique linéaire)
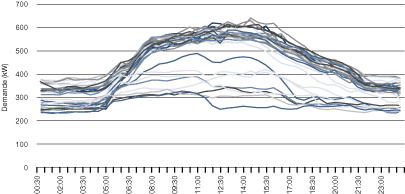
[version textuelle - Figure 23a]
Figure 23b. Profil typique de la demande aux 30 minutes (tracé de contours)
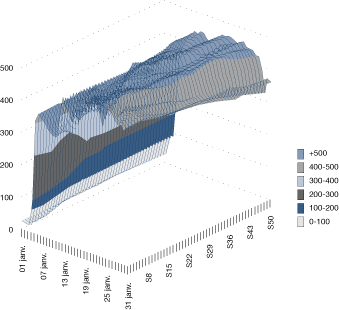
[version textuelle - Figure 23b]
8.4 Calcul des indicateurs de rendement
Dans certains cas, on peut mesurer le rendement de l'énergie en utilisant une mesure simple, comme la consommation d'énergie d'un secteur ou d'un procédé. Toutefois, cette consommation est souvent fortement influencée par des facteurs externes comme le taux de production, auquel cas on peut utiliser la « consommation d'énergie spécifique », c'est-à-dire la consommation d'énergie divisée par le taux de production.
Il faut interpréter très soigneusement ce type de mesure. Un procédé à demande élevée d'énergie de base aura, par exemple, une consommation spécifique plus faible lorsque le taux de production est élevé, même si l'efficacité de base des opérations demeure inchangée.
D'autres indicateurs d'efficacité peuvent aussi être utilisés, comme l'efficacité d'une chaudière ou le coefficient de performance (COP) d'un système de réfrigération. On s'attend à ce que ces valeurs varient elles aussi (notamment l'efficacité de la chaudière selon la pression de vapeur, et le COP selon la température ambiante).
Les indicateurs de rendement sont utiles. Toutefois, ils devraient être comparés aux valeurs cibles, notamment :
- aux valeurs cibles obtenues par modélisation des opérations;
- aux valeurs cibles fondées sur la production d'une usine ou de procédés dans des conditions semblables (soit à partir de données historiques de la même installation ou du même procédé, soit d'un autre procédé très semblable).
8.5 Compréhension de la variabilité du rendement : Techniques simples
Un certain nombre de techniques simples permettent de comprendre la variabilité de la consommation d'énergie. La variabilité peut être présentée sous forme d'une distribution de fréquences qui permet de visualiser la valeur moyenne, la fourchette (ou l'écart type) et la forme de la distribution.
Figure 24. Exemple de la distribution de fréquences
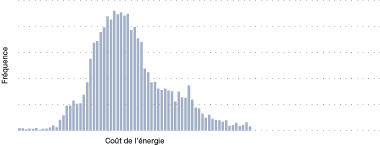
[version textuelle - Figure 24]
La figure 24 illustre un exemple typique du coût spécifique de l'énergie d'un procédé. On dénote une importante fourchette qu'une analyse chercherait à expliquer. Des facteurs externes ou une décision prise par les responsables des opérations pourraient en être à l'origine.
Une courbe illustrant la consommation d'énergie en fonction des facteurs déterminants peut permettre de dégager certaines relations; par exemple, on peut tracer la consommation en fonction de la production pour obtenir une relation bien définie (voir la figure 25).
Figure 25. Consommation d'énergie en fonction de la production
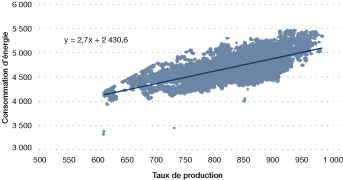
[version textuelle - Figure 25]
Le diagramme de la figure 25 indique également :
- que la consommation de base est de 2 430,6 unités;
- qu'il y a une variabilité résiduelle : le taux de production n'explique pas entièrement les variations de consommation (en fait, la variabilité résiduelle est importante).
Une analyse de régression linéaire permet d'établir que la relation en question peut être décrite par une équation de la forme suivante :
y = mx + c, y = 2,7x + 2 430,6
où
y = consommation d'énergie
x = taux de production
m = pente de la courbe
c = ordonnée à l'origine
Il est possible d'étendre l'analyse à un graphique en trois dimensions (voir la figure 26).
Figure 26. Exemple d'un graphique tridimensionnel de la consommation d'énergie en fonction de la production et de la qualité de l'alimentation
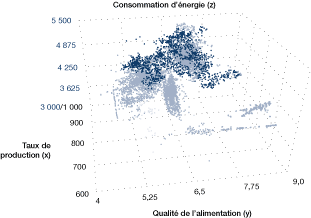
[version textuelle - Figure 26]
Grâce à des techniques de régression multiple, on peut obtenir des équations plus détaillées pour décrire les relations.
y = m1 x1 + m2x2 + m3x3 + ... + c
Il existe sur le marché des logiciels permettant d'effectuer ces calculs et d'obtenir ces graphiques facilement. Les chiffriers courants possèdent toutes ou presque toutes les capacités nécessaires pour effectuer ces analyses.
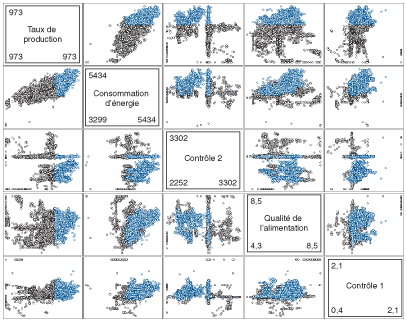
Il est parfois difficile de dégager des tendances à partir des tracés comportant de nombreuses variables. Les diagrammes de dispersion bidimensionnels multiples facilitent l'établissement des rapports entre des variables multiples (tracés de type matrice) en illustrant, d'un coup d'œil, les relations entre les données. Dans la figure 27, les cellules ombragées indiquent les valeurs d'axe pour chacune des variables tracées. La première cellule non ombragée dans la première rangée donne le taux de production sur l'axe des y en fonction de la consommation d'énergie sur l'axe des x. La première cellule dans la dernière rangée donne la variable contrôlable « Contrôle 1 » sur l'axe des y en fonction du taux de production. Les données représentant une consommation élevée apparaissent en bleu pâle. À titre d'exemple des relations qu'il est possible de dégager de ces diagrammes de dispersion bidimensionnels multiples, citons la relation bien claire entre la consommation d'énergie et la qualité de l'alimentation. Autre exemple de consommation élevée : les valeurs inférieures de la variable contrôlable
« Contrôle 2 ».
Figure 27. Diagramme de dispersion multiple
[version textuelle - Figure 27]
8.6 Compréhension de la variabilité du rendement : Exploration des données
Parfois, une analyse plus détaillée convient mieux :
- aux grands consommateurs d'énergie;
- lorsque la consommation d'énergie représente un enjeu complexe qui dépend d'une multitude de facteurs déterminants;
- lorsque l'on a accès à une grande quantité de données historiques provenant, notamment, d'une base de données d'archivage des données.
L'exploration de données présente les caractéristiques suivantes :
- elle permet de manipuler des bases de données énormes;
- elle recherche automatiquement les relations;
- elle présente ces relations sous forme d'ensemble de règles.
L'arbre de décision illustré à la figure 28 représente un ensemble de règles produites lors d'une analyse d'exploration de données. Les règles permettent de mettre en valeur le facteur clé de consommation d'un système de réfrigération et de déterminer l'ampleur de l'impact de cet élément. Le « cheminement » surligné dans l'arbre est caractérisé par la règle suivante :
Si la température du solvant > 223 °C et < 214 °C
D'après la probabilité estimée à 86,67 p. 100 dans la fenêtre « Attributs », dans la partie droite de la figure 28, la consommation a été déterminée par analyse à 67 167 unités dans les conditions indiquées.
Les règles sont produites automatiquement dans ce type d'analyse. L'utilisateur définit uniquement les objectifs et les facteurs déterminants. Essentiellement, le processus répartit les activités historiques en modes; lorsque la consommation est différente, les modes sont déterminés par des règles.
Figure 28. Arbre de décision simple

[version textuelle - Figure 28]
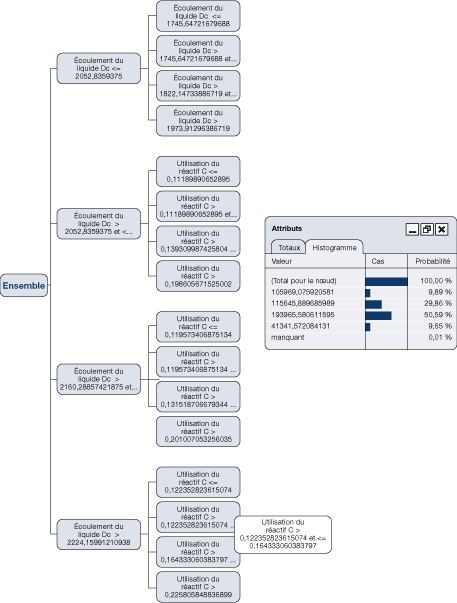
Une analyse de données réelles produira des arbres de décision beaucoup plus complexes – car les règles sont plus complexes – comme celui de la figure 29. Ce type d'arbre indiquera :
- les éléments clés;
- l'ampleur de l'effet sur la consommation d'énergie;
- les meilleurs modes de fonctionnement.
La figure 29 illustre un cheminement « en nœud » pour le débit du liquide et l'utilisation d'un réactif selon lequel il y aurait une probabilité de 50,59 p. 100 que la consommation d'énergie soit de 193 965 unités dans ces conditions.
Figure 29. Arbre de décision complexe
[version textuelle - Figure 29]
Les outils d'exploration de données sont répandus et couramment utilisés. La figure 30 illustre les étapes typiques d'une telle analyse.
Figure 30. Étapes d'une analyse initiale d'exploration des données

[version textuelle - Figure 30]
Ces étapes font partie de tout projet d'analyse approfondie des données.
Exemple 2 : Rendement d'une installation de chaudières à haute pression
On a analysé l'efficacité d'une installation de chaudières à haute pression. Cette installation comprend trois chaudières, dont deux fonctionnent en temps normal. Les chaudières peuvent être alimentées au gaz naturel ou au mazout et peuvent produire de la vapeur sous une pression manométrique maximale de 1 600 lb/po2 (11 MPa) pour alimenter des turbines à vapeur et d'autres systèmes fonctionnant sous une pression plus faible.
Les données ont été recueillies à l'installation après une modification des systèmes de surveillance, puis elles ont été explorées en mettant l'accent sur le coût d'exploitation par unité de vapeur.
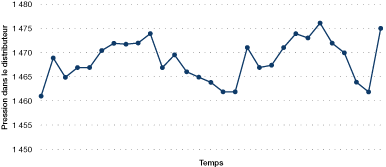
Figure 31. Pression de vapeur dans le distributeur de la chaudière
[version textuelle - Figure 31]
Les attributs comprennent la sélection des chaudières dans la séquence d'exploitation, les charges, les pressions, les températures et les débits de vapeur prélevée dans les turbines.
La figure 31 illustre la pression de vapeur dans le distributeur de la chaudière sur une période de 30 minutes.
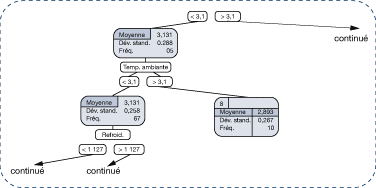
L'incidence de la pression dans le distributeur sur le coût d'exploitation est indiquée dans l'arbre de décision partiellement illustré à la figure 32. Dans cet exemple, une pression de vapeur plus élevée réduit le coût d'exploitation par unité de vapeur produite. En comparaison, la figure 33 indique que des tracés du coût en fonction de la pression de vapeur dans le distributeur ne permettent pas d'illustrer clairement l'influence de la pression, et ce, en raison des changements dans les ensembles de données, qui résultent de nombreux autres facteurs influant sur le rendement.
Figure 32. Incidence de la pression dans le distributeur sur les coûts d'exploitation – arbre de décision partiel
[version textuelle - Figure 32]
Figure 33. Coûts en fonction de la pression dans le distributeur
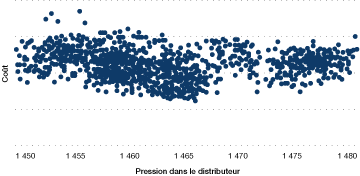
On a relevé, au total, une possibilité de diminuer les coûts annuels de 4 p. 100 (d'une valeur d'environ 500 000 $), ce qui correspond à une période de récupération d'un an.
[version textuelle - Figure 33]
8.7 Calcul des objectifs
Les objectifs sont les valeurs de rendement prévues que l'on peut comparer au rendement réel pour déterminer si une installation ou un procédé affiche ou non un bon rendement. Ils se présentent sous plusieurs formes, dont les suivantes :
- Le rendement moyen obtenu à partir de données historiques est un objectif couramment utilisé. Il permet d'avertir le personnel opérationnel lorsque le rendement est inférieur à la moyenne.
- La forme la plus simple de ce type d'objectif est la consommation moyenne au cours d'une période antérieure, par exemple au cours de l'année ou du mois précédent.
- Il arrive souvent que les objectifs doivent être ajustés pour tenir compte de facteurs externes, comme le taux de production ou la température ambiante. En général, cet ajustement est apporté à la suite d'une analyse de régression simple ou multiple.
Dans certains cas, l'objectif est ajusté pour indiquer l'intention d'apporter une amélioration. Par exemple, il peut être modifié pour obtenir une autre réduction de consommation de 5 p. 100 dans l'ensemble des installations.
L'exactitude et la robustesse des objectifs sont extrêmement importantes. Un objectif incorrect induira en erreur; les améliorations ne paraîtront peut-être pas dans les calculs, ou encore un faible rendement ne sera pas repéré. Des objectifs inadéquats entraînent une perte de confiance à l'égard du processus de surveillance et se traduira par une incapacité à réaliser des économies d'énergie.
On peut obtenir un objectif plus précis basé sur des données historiques grâce à l'exploration de données et à d'autres techniques semblables. De cette façon, un plus grand nombre de données peuvent être analysées, plus de facteurs déterminants peuvent être pris en compte et il est plus probable que les relations non linéaires pourront être exploitées.
Figure 34. Rendement réel et rendement prévu en fonction du temps
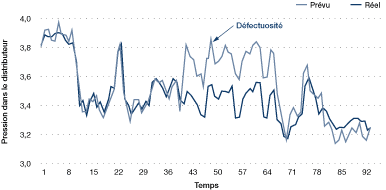
[version textuelle - Figure 34]
Un objectif obtenu grâce à une analyse détaillée des données recueillies (p. ex., aux heures ou aux 15 minutes) peut être suffisamment précis pour être appliqué en ligne, en temps réel. Cette méthode a pour avantage, entre autres, de déceler plus rapidement les problèmes de fonctionnement. Les gros consommateurs d'énergie devraient envisager de faire appel à ce genre d'approche.
Le rendement moyen historique peut servir de point de référence par rapport au rendement ultérieur. Il représente ce qui se serait produit si aucun changement (amélioration) n'avait été apporté.
Un objectif optimal indique ce qu'un procédé ou une installation bien exploitée pourrait réaliser. Il diffère du rendement historique moyen et d'une amélioration recherchée, car il a été établi à partir de données sur le potentiel d'amélioration.
On peut calculer la valeur cible optimale à partir de principes de base, auquel cas cette valeur représente la valeur théoriquement possible. La modélisation informatique est fréquemment appliquée aux principaux procédés comme le raffinage du pétrole et la fabrication de produits pétrochimiques, et elle est utilisée de plus en plus souvent dans d'autres secteurs. On procède également à la modélisation de systèmes comme les chaufferies et les installations de réfrigération.
Il se peut aussi que les objectifs optimaux représentent le meilleur rendement déjà atteint compte tenu des conditions particulières (externes), ce que peut permettre de déterminer l'analyse de données d'exploitation antérieures à l'aide de techniques d'exploration de données et d'autres techniques semblables.
Selon cette approche, on détermine les périodes d'exploitation antérieures au cours desquelles les conditions externes étaient semblables aux conditions actuelles, puis on choisit comme objectif les résultats de la période où le rendement était maximal. Il existe des logiciels qui permettent d'automatiser cet exercice.
Le rendement par rapport à l'objectif peut être exprimé de différentes façons. On peut signaler un faible rendement par rapport à l'objectif au fur et à mesure qu'il se révèle, par exemple en termes de coût annuel si les défectuosités ne sont pas réparées.
Figure 35a. Rapport sur le rendement
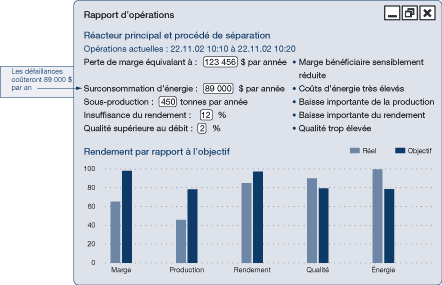
[version textuelle - Figure 35a]
Figure 35b. Rapport des sommes cumulées (graphique linéaire simple)
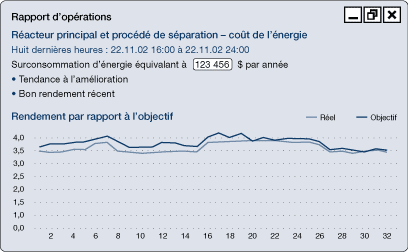
[version textuelle - Figure 35b]
Figure 35c. Rapport des sommes cumulées (résumés mensuels,hebdomadaires ou annuels)
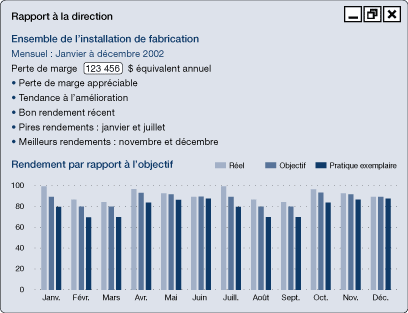
[version textuelle - Figure 35c]
Les techniques de sommes cumulées mettent en évidence les économies cumulées pendant une période. Par exemple, la figure 36 montre les économies cumulées pendant huit semaines.
Figure 36. Rapport des sommes cumulées
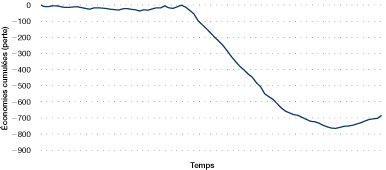
[version textuelle - Figure 36]
Les valeurs des sommes cumulées sont établies en faisant la somme des économies réalisées pendant chaque période afin d'obtenir un total cumulatif en évolution. Lorsque l'objectif assigné au procédé est atteint, le total cumulatif des économies sera en moyenne de zéro et la courbe du graphique sera horizontale. Un rendement insatisfaisant entraînera des pertes au cours de chaque période et la pente de la ligne sera négative. Un rendement dépassant l'objectif produira une pente positive. Tout changement de pente sur un graphique des sommes cumulées correspond à un « événement », soit une modification du rendement du procédé.
8.8 Modélisation des données et analyse par simulation/anticipation
Dans cette technique, on établit les objectifs en élaborant un modèle des opérations à l'aide de données historiques d'exploitation (ou un modèle de principes de base).
D'autres techniques de modélisation peuvent être envisagées, dont des techniques neuromimétiques, des techniques de raisonnement par cas ou diverses techniques mathématiques et statistiques. Ces techniques devraient être utilisées avec précaution : la modélisation des procédés demande de la part de l'analyste une bonne compréhension des relations entre les variables. L'induction de règles facilite cette compréhension.
En dépit des obstacles, la modélisation des données peut s'avérer efficace pour la surveillance des dispositifs de contrôle et d'optimisation. De plus, les modèles peuvent servir à étudier l'effet de conditions anormales grâce à l'analyse par simulation/anticipation.
Détails de la page
- Date de modification :