Annexe D : Formules pratiques
Calcul de la puissance nécessaire à une charge
La charge mécanique nécessaire à l'équipement entraîné est appelée la puissance au frein (BHP). La valeur de la BHP peut se calculer comme suit :
avec : HP = puissance fournie par le moteur
T = force de rotation (lb·pi) x rayon
N = vitesse de référence du moteur (tr/min)
Après détermination de la puissance au frein nécessaire de la machine (produit de la vitesse par le couple), la puissance en HP peut être déterminée :
Si la puissance calculée se situe entre deux puissances assignées de moteur normalisées, choisir la puissance assignée la plus élevée. C'est là une bonne pratique de garder une certaine marge lors du choix de la puissance d'un moteur.
Dans bien des applications, il est possible de calculer la puissance nécessaire sans avoir mesuré réellement le couple nécessaire.
Quelques exemples types :
Pour les convoyeurs
Pour les ventilateurs et soufflantes
Effet de la vitesse sur la puissance.
HP = k1 x vitesse (tr/min)³ - la puissance varie comme le cube de la vitesse
Débit = k3 x vitesse (tr/min) - le débit varie proportionnellement à la vitesse
Pression totale = pression statique + pression dynamique
Pression dynamique = V2 x (1/1096,7)2 x densité
Pour les pompes
Densité relative de l'eau = 1
1 pi3 par seconde = 448 gallons/min
1 PSI = une hauteur de 2309 pi pour une eau pesant 62,36 lb/pi3 à 62 °F
Pompes à cylindrée constante
Effet de la vitesse sur la puissance (HP) = k x vitesse (tr/min).
La puissance et la capacité varient directement avec la vitesse.
Les pompes volumétriques sous hauteur constante nécessitent un couple sensiblement constant à toutes les vitesses.
Pompes centrifuges
Effet de la vitesse sur la puissance au frein absorbée.
HP = k1 x vitesse (tr/min)3 - la puissance varie comme le cube de la vitesse
T = k2 x vitesse (tr/min)2 - le couple varie comme le carré de la vitesse
Débit = k3 x vitesse (tr/min) - le débit varie proportionnellement à la vitesse
Rendement d'une pompe centrifuge (type)
500 à 1000 gal/min = de 70 % à 75 %
1000 à 1500 gal/min = de 75 % à 80 %
Plus de 1500 gal/min = de 80 % à 85 %
Le rendement des pompes volumétriques peut varier entre 50 % et 80 %, selon leur puissance.
Puissance nécessaire
Loi d'Ohm
Volts = ampères x ohms
Puissance dans les circuits c.c.
Watts = volts x amperes
Puissance dans les circuits c.a.
Kilovoltampères (kVA)
Kilowatts (kW)
Circuits triphasés c.a
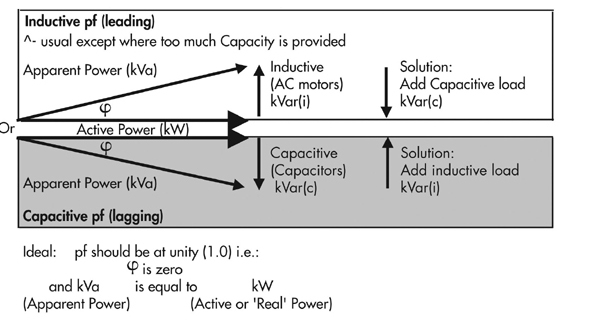
Figure 23: Triangle des puissances
Figure 23 : Triangle des puissances - Illustration des relations entre :
- Puissance active (kW) et puissance apparente (kVA)
- Le rapport de la puissance active à la puissance apparente est le facteur de puissance (kW/kVA)
- Charge inductive et charge capacitive (kVar)
- Circuit inductif (tension en avance) et à circuit capacitif
(tension en retard)
Usual except where too much capacity is provided
Apparent Power (kVA)
Inductive (AC motors) kVar (i)
Solution: Add Capacitive Load kVar (c)
Active Power
Apparent Power (kVA)
Capacitive (Capacitors) kVar (c)
Solution: Add inductive Load kVar (i)
Capacitive pf (lagging)
Ideal: pf should be at unity (1.0) i.e.
φ is 0
and kVA (Apparent power)
is equal to
kW (Active or 'Real Power')
Cas général sauf si le circuit est fortement capacitif
Puissance apparente (kVA)
Inductive (moteurs c.a.) kVar (i)
Solution : ajouter une charge capacitive kVar (c)
Puissance active
Puissance apparente (kVA)
Capacitive (condensateurs) kVar (c)
Solution : ajouter une charge inductive kVar (i)
Facteur de puissance capacitif (en retard)
Idéalement : PF devrait être égal à 1, c.-à-d. :
φ est nul
et la puissance apparente (kVA)
est égale à
la puissance active ou 'réelle' (kW)
Détails de la page
- Date de modification :